L'objectif de ce TP est d'explorer la problématique du remaillage régulier de surfaces polyédrales. Le présent document est structuré en trois parties, chacune correspondant au travail à réaliser pendant une séance de TP. Ce découpage est cependant arbitraire, n'hésitez pas à le dépasser suivant vos envies ou vitesse de progression.

TP 5 : implémentation d'un octree

Comme l'indique wikipédia, Un octree est une structure de données de type arbre dans laquelle chaque nœud peut compter jusqu'à huit enfants. Les octrees sont le plus souvent utilisés pour partitionner un espace tridimensionnel en le subdivisant récursivement en huit octants.

Il existe dans CGAL une implémentation des octree (AABB tree), qui permet de calculer rapidement des intersections et calculs de distance. L'interface telle qu'elle est proposée dans la documentation ne permet pas d'accéder explicitement à la structure de données interne. Or, dans le suite de ce TP, on aura besoin d'avoir accès aux sommets contenus dans chacune des feuilles de l'octree.

On se propose donc de développer notre propre structure de données permettant de distribuer les sommets d'un maillage dans un octree, afin de l'utiliser pour la simplification de maillages. Cette implémentation devra notamment permettre de :

• Choisir le nombre maximum de sommets que pourra contenir une feuille de l'arbre (typiquement, on peut choisir une valeur de 50).
• Choisir avant sa construction la profondeur maximum de l'arbre (typiquement, on peut choisir une valeur de 5). C'est la profondeur maximum qui « gagne » sur le nombre maximum de sommets.
• Peupler à partir d'un maillage un arbre, en utilisant une boîte englobante alignée sur les axes XYZ, et en la divisant de manière itérative en 8 feuilles.
• Donner un moyen d'accéder à la liste des sommets contenus dans une feuille de l'arbre.
• Donner la feuille de l'arbre qui contient un sommet donné (grâce à sa coordonnée).

On pourrait raconter l'algorithme de cette manière :

• Calculer la boîte englobante du maillage, et initialiser l'arbre avec un seul nœud, de profondeur 0, et dimensionné suivant cette boîte englobante.

• Pour chaque sommet du maillage

  • Considérer le fait d'ajouter le sommet dans le nœud racine de l'arbre ;
  • Si ce nœud n'est pas une feuille, descendre dans l'arbre en choisissant à chaque fois la boîte englobante qui contient le sommet que l'on doit ajouter. Considérer le fait d'ajouter le sommet dans le nœud feuille qui lui correspond.
  • Si ce nœud a atteint le nombre maximum de sommets, mais n'est pas à la profondeur maximum, lui fabriquer 8 fils, descendre tous les sommets (y compris le nouveau) dans leur feuille respective (on peut avoir besoin de répéter l'opération plusieurs fois si tous les sommets sont dans le même fils).

Remarques :

• Pour faciliter la visualisation, et la compréhension de votre maillage, vous pouvez utiliser une profondeur d'arbre réduite (typiquement 2 ou 3).

Plusieurs pistes d'aide à la réflexion :

• On accède aux coordonnées d'un sommet en utilisant les fonctions vertex->point().x(), .y() et .z(), de la classe Point_3.
• La structure de données peut contenir pour chaque nœud sa boîte englobante (décrite par le minimum et maximum des coordonnées x, minimum et maximum des coordonnées y, et minimum et maximum des coordonnées z), une liste de ses 8 nœuds fils (liste vide si c'est un nœud feuille), et une une liste de Vertex_handle qui sera vide sauf pour les nœuds feuille.
• Mieux qu'une liste de nœuds, on peut avoir une liste de liste de liste de nœuds, afin de pouvoir accéder à chaque fils avec fils[x][y][z], où x, y et z sont entiers (0 ou 1) correspondant pour chaque coordonnée au côté où le sommet se situe par rapport à l'axe médian de la boîte. On pourra aussi utiliser une liste de fils, et utiliser un 4 * x + 2 * y + z pour accéder à son élément suivant les trois décisions des axes médians.
• On pourra aussi associer à chaque nœud une adresse composée d'une liste de trois booléens. La racine est située à l'adresse liste vide, son premier fils à l'adresse ((0, 0, 0)), le second fils de son premier fils à l'adresse ((0, 0, 0), (1, 0, 0)), etc. Cela peut être un outil facilitant pour l'identification de chaque nœud dans l'arbre.

TP 6 : visualisation d'un octree

Dans cette partie du TP, on se propose de fabriquer un fichier au format OFF, dont les formats sont colorés en fonction de leur nœud d'appartenance.

Le format OFF est un format très simple, au format ascii, dont on trouve la spécification standard en ligne. Ce format permet par défaut de stocker des coleurs sur les faces. Si l'on veut stocker les couleurs sur les sommets, il est nécessaire d'implémenter une variante. Dans ce cas, l'entête n'est plus "OFF" mais "COFF", et chaque ligne de sommet est décrite sous la forme «x y z r g b», où r, g et b sont des réels entre 0 et 255 décrivant la composante rouge, verte et bleue du sommet. Le fichier vertcube.off en donne un exemple.

Remarque : le plus simple est de fabriquer ce fichier à la volée, en utilisant un itérateur sur les sommets du maillages, puis un itérateur sur les faces du maillage, et en écrivant dans un fichier, à la manière du TP précédent.

Extension possible : une autre manière de visualiser la construction de l'octree est de générer un maillage qui contienne un pavé droit pour chacun des nœuds feuille non vide (correspondant à sa boîte englobante). On observera ainsi des petits cubes aux endroits où il y a beaucoup de détails géométriques, et de grands cubes là où il y en a peu.

TP 7 : simplification d'un maillage par octree

Maintenant que l'on dispose d'une structure de données octree, on a un moyen d'avoir une version simplifiée du maillage.

On fabrique un nouveau maillage de la manière suivante :

• Tous les sommets appartenant à une même feuille de l'octree sont fusionnés ;
• Les faces conservées sont celles du maillage initial qui après fusion des sommets sont non dégénérées (on ignore les faces à 1 ou 2 sommets).

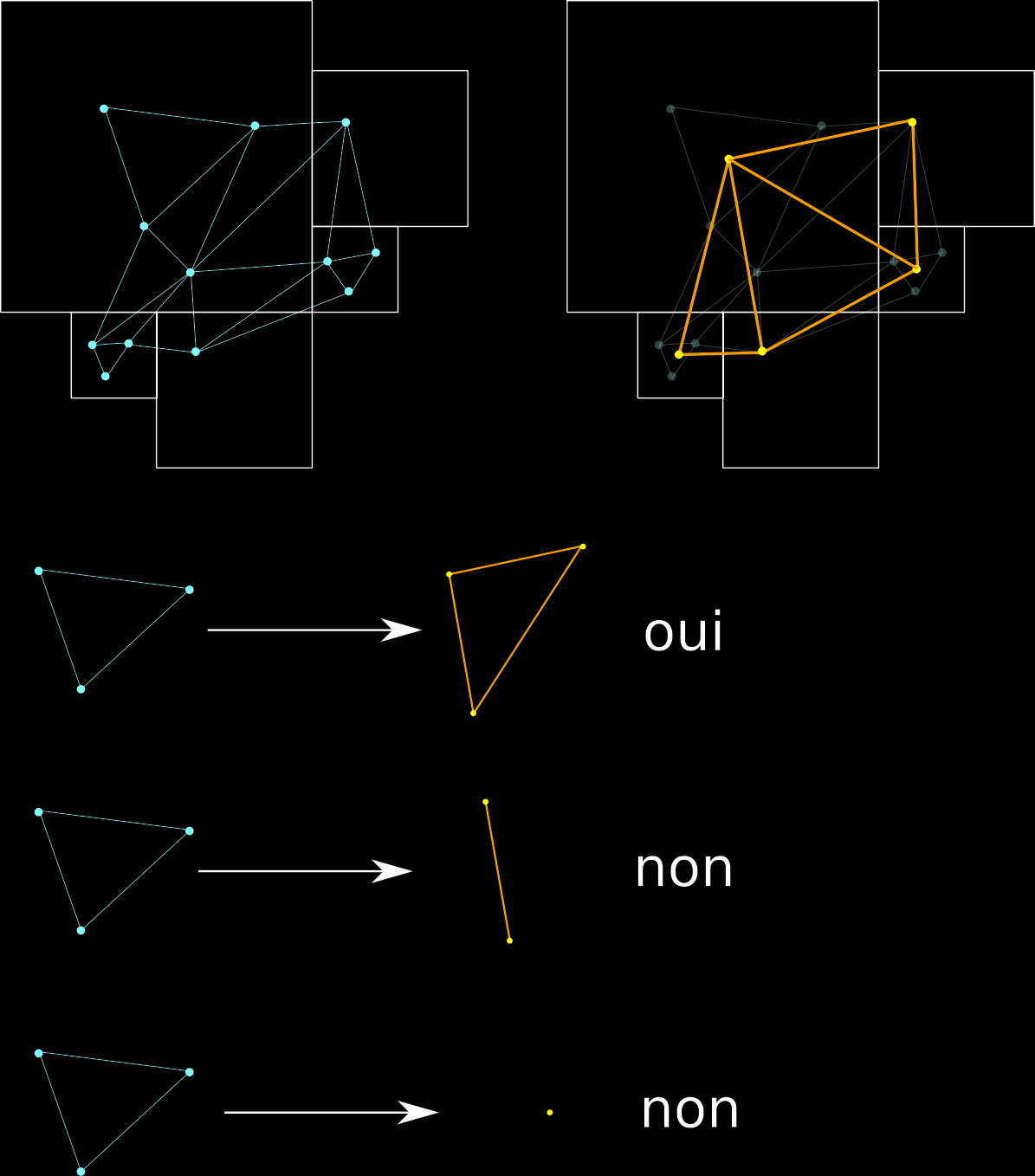
Remarques :

• On rencontre parfois des faces en double (deux faces ont exactement les mêmes sommets dans le maillage généré). Il s'agit probablement de triangles en trop, correspondant à un repli de la surface. Une bonne stratégie consiste alors à supprimer les deux.
• Une question reste ouverte, et le rendu final en sera très dépendant : comment choisir la position du point qui représentera tous les sommets d'une feuille ?
• Comme dans le cas de la fabrication d'un maillage coloré, il peut être plus simple de générer un fichier OFF correspondant à cette simplification sans construire en mémoire un nouveau maillage CGAL.
• Dans le cas de géométries complexes, il est possible que la topologie du maillage obtenu soit incorrecte, avec des sommets dont les faces adjacentes ne forment pas un voisinage cohérent. CGAL pourrait avoir des problèmes à charger ce nouveau maillage, mais meshlab saura l'afficher.
• Si le maillage que vous manipulez a peu de sommets (quelques milliers par exemple), il peut être intéressant de diminuer le nombre de sommets maximum par feuille pour obtenir un résultat un tout petit peu intéressant.

Sujets d'exploration :

• Que se passe-t-il quand on change la profondeur de l'arbre ? Quand on change le nombre maximum de sommets par cube ?
• Est-ce que tous les maillages sont pris en charge de manière efficace par cette méthode ? Quels types de maillages faut-il privilégier ?
• Pour le placement du sommet de la feuille, on peut explorer plusieurs solutions : centre de la boîte englobante de la feuille, moyenne de la position des sommets contenus dans la feuille, sommet contenu dans la feuille le plus proche de cette moyenne, etc. À vous d'explorer la solution la plus intéressante, en vous demandant combien cela déforme ou non l'allure générale du maillage.
• Pour aller plus loin, on peut aussi envisager de re-subdiviser chaque feuille dans le cas où le morceau de surface qu'elle contient n'est pas plat (proche d'être un plan). Une approche consiste à calculer les angles diédraux des arêtes du cube, et de décider par seuillage de leur moyenne si l'on subdivise ou non la feuille.

Ressources

La méthode que vous avez implémentée est pertinente sur des maillages avec un grand nombre de sommets. En plus des maillages déjà proposés, voici quelques éléments supplémentaires qui pourraient vous être utiles :

• Maillages.zip, avec notamment le maillage strange.off contenant beaucoup de sommets.
• tore-carre.off, qui a des faces de taille variées.
• meshes.tbz2, qui contient notamment des maillages scannés, aux résolutions variées (certains avec des milliers de sommets), mais qui pourraient contenir des défauts topologiques, impossibles à charger par CGAL (à vérifier).

Vous pouvez aussi fabriquer des maillages avec une configuration spécifique, pour illustrer une intuition que vous avez sur l'algorithme.

Un début de structure de classe discuté en cours : sur pastebin.