Introduction au seuillage

Dans la séance précédente, nous avons calculé différentes mesures sur les faces, telle que leur périmètre. La visualisation par dégradés de couleur n'est pas toujours simple à lire. Nous allons donc explorer la piste du seuillage : séparer les faces en deux classes suivant que leur valeur est plus grande ou plus petite que le seuil choisi.

Travail à réaliser : écrire une fonction qui calcule pour chaque face un identifiant (entier) suivant qu'il est dans l'une ou l'autre des deux classes de cette segmentation, en ayant fixé le seuil par une méthode simple (par exemple la moyenne des mesures calculées par les faces).

où l'on aura défini Facet_double_map par typedef std::map<Polyhedron::Facet_handle, double> Facet_double_map;, et Facet_int_map par typedef std::map<Polyhedron::Facet_handle, int> Facet_int_map;.

Remarque : on pourrait le faire avec plus de deux classes, en ayant plusieurs seuils.

Génération de maillages colorés

Pour visualiser cette segmentation, une piste consiste comme lors de la séance passée à sauver le maillage dans un fichier où les identifiants des régions sont traduits en couleur.

Travail à réaliser : adapter la fonction écrite lors de la séance précédente en générant de manière aléatoire une couleur par identifiant de région. Vérifier à l'aide de MeshLab que la segmentation produite est cohérente sur vos maillages de test.

Remarque : on souhaite que la fonction prenne aussi en charge les segmentations à n>2 classes.

Indications : on pourra utiliser un map qui associe à un entier une couleur RGB. À chaque nouvelle facette rencontrée, on regarde si une couleur a déjà été stockée pour son identifiant de région. Si ce n'est pas le cas, on en génère une, sinon, on utilise celle qui a été stockée.

Intégration des composantes connexes

En observant le résultat de cette segmentation sur différents maillages, on observe qu'à la surface de l'objet, plusieurs composantes connexes sont colorées de la même couleur. On se propose donc, étant donné une segmentation, de produire une nouvelle segmentation qui respecte l'originale, tout en attribuant à chaque composante connexe originale un identifiant différent.

Exemple : si un objet de forme alongée est composé de grandes faces au centre, et de petites faces aux deux extrémités, une première segmentation par seuillage à partir du périmètre aura produit deux classes de faces (les petites et les grandes). Une fois introduite la notion de composante connexe, on aura alors trois classes : une classe par extrémité, et une classe centrale.

Travail à réaliser : écrire une fonction qui étant donné un maillage et une segmentation produit une nouvelle segmentation qui sépare en différentes classes les composantes connexes de la segmentation initiale.

Indications : on va parcourir le maillage, en regardant successivement toutes les facettes. Pour chaque facette, si elle n'a pas été vue, on la marque comme vue, puis on parcours les facettes voisines, avec un appel récursif si elles sont dans la même classe de segmentation que la première facette. On peut utiliser pour ça un parcours des demies-arêtes autour de la face, et pour chacune de ces demie-arêtes, on utilise opposite() pour obtenir la demie-arête opposée, puis facet() pour obtenir la facette adjacente.

Choix du seuil

Le choix du seuil est une question complexe. L'utilisation d'une moyenne comme évoquée plus haut est peu satisfaisante. En traitement d'images, une technique classique consiste à utiliser la méthode d'Otsu (la wikipédia anglaise est plus claire sur la technique de calcul) pour fixer automatiquement un seuil. Dans cette méthode, on commence par calculer un histogramme de la valeur à seuiller, puis on calcule le seuil optimal à l'aide de la variance des deux classes. Afin d'adapter cette technique au cas des maillages, il est important de calculer un histogramme pondéré, où chaque face « pèse » en fonction de son aire dans l'histogramme.

Travail à réaliser : écrire une fonction qui prend en entrée un maillage et une propriété locale calculée pour chaque face, et qui fixe automatiquement le seuil à partir de la méthode d'Otsu.

Indications : on a calculé sur un maillage une mesure (par exemple le périmètre), notée m[f] pour chaque face f. Un histogramme est donc construit, constitué d'un tableau (de taille fixée, par exemple 64) où chaque entrée correspond à la quantité de la surface pour laquelle la mesure est inclue. Une face f contribuera alors à la classe correspondant à sa mesure m[f] à hauteur de son aire a[f], qu'il faudra calculer.

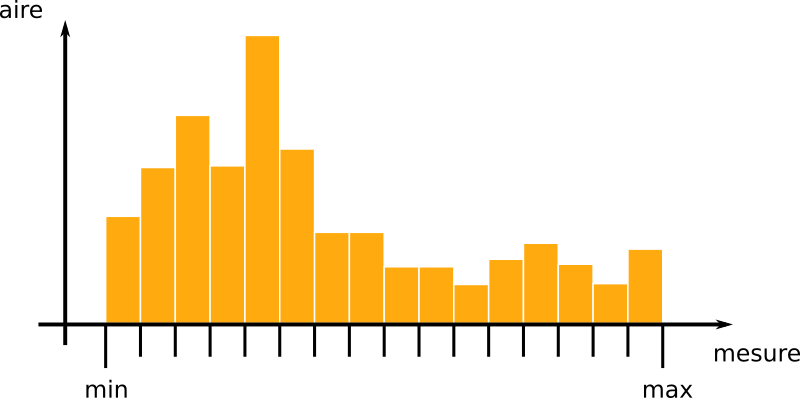
On applique ensuite la méthode de Otsu à cet histogramme pour estimer un seuil de séparation pertinent entre deux classes suivant la mesure donnée en paramètre.

Expérimentations

Chaîne de traitement complète : à partir de différentes mesures locales réalisées au TP précédent, utiliser la méthode de Otsu pour calculer automatiquement un seuil de segmentation. Produire une première segmentation en deux classes qui respecte ce seuil. Intégrer ensuite la notion de composantes connexes afin de produire une segmentation plus précise de l'objet.

Expérimenter cette segmentation sur différents objets, et avec différentes mesures locales, en utilisant meshlab pour visualiser la coloration que vous aurez réalisée.

Question : quelles conclusions peut-on tirer de ces expérimentations ? Quel choix de mesure locale est plus intéressant ? Est-ce que cela dépend du type de maillage traité ? Appuyez-vous sur des captures d'écrans de maillages colorés pour argumenter votre propos.

En début de séance, vous aviez utilisé un calcul de seuillage plus simple, en utilisant la moyenne des valeurs comme valeur seuil. Comparez les segmentations obtenues par votre chaîne de traitement en utilisant d'un côté la méthode de Otsu, et de l'autre côté la moyenne.

Question : la méthode de Otsu, plus complexe à implémenter, apporte-t-elle une segmentation plus intéressante ? Appuyez-vous sur des captures d'écrans de maillages colorés pour argumenter votre propos.