Introduction à la géométrie discrète
Jean-Marie Favreau — ISIMA 3ème année F1
cette première séance fait partie du module géométrie algorithmique
sauf remarque contraire, les images sont issues de http://blender.org
Outils mathématiques pour la modélisation
la géométrie, c'est de la belle mathématique
Représenter la réalité
on vit dans un monde en 3D
géométrie

matériaux
 Substance, Allegorithmic
Substance, Allegorithmic
mouvement


- contraintes de rotation, position, taille
- armature, treillis (lattice)
- clés de mouvement (keyframes)
Ce que proposent les modeleurs 3D
intéressons-nous à la géométrie
surfaces paramétriques


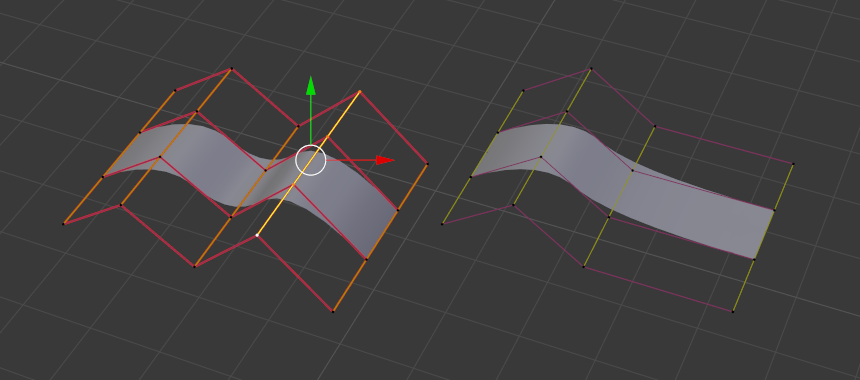
Bézier, NURBS
particules

liquides, gaz, tissus, cheveux, ...
maillages

Pourquoi utiliser des maillages ?
parfois, il faut savoir justifier ses marottes
Motivations mathématiques
quand on y pense
profiter de formalismes existants
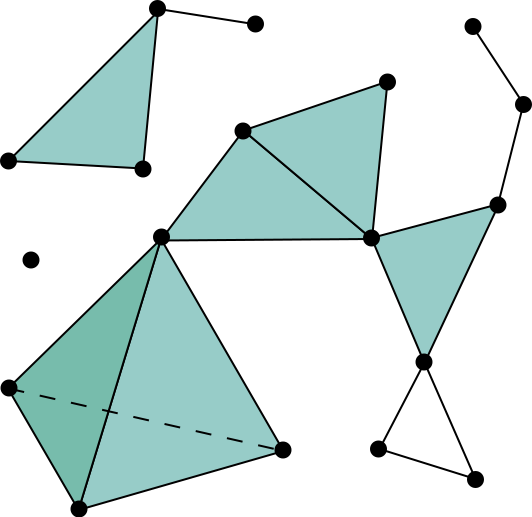
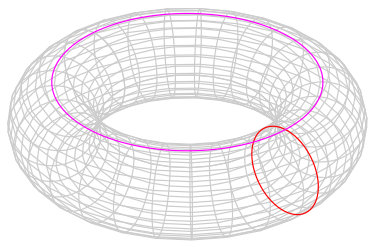

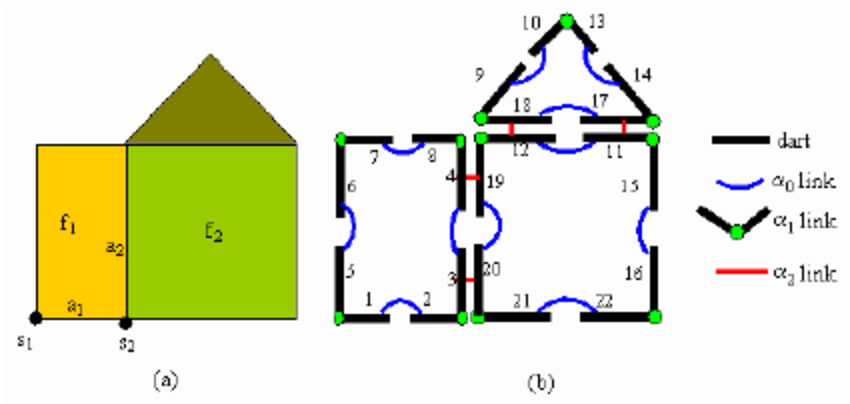
complexes simpliciaux, groupes d'homotopie, groupes d'homologie, cartes généralisées
décrire toutes les topologies

genre : 8
Motivations pratiques
quand on en fait
grande flexibilité de l'outil
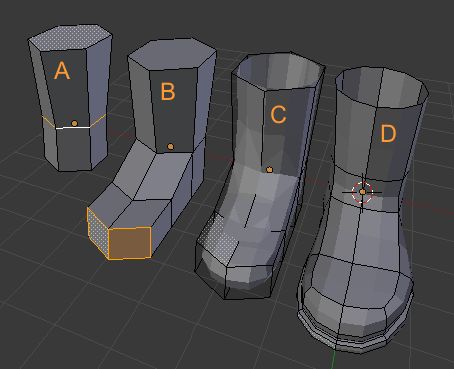
Extrusion, subdivision, lissage, découpage, couture, ...
sculpture, low-poly, rendu performant



Normal map, bump map et displacement maps
Quelques exemples de maillages
ouvrir les yeux au monde numérique
infographie
jeux vidéos, films, serious game


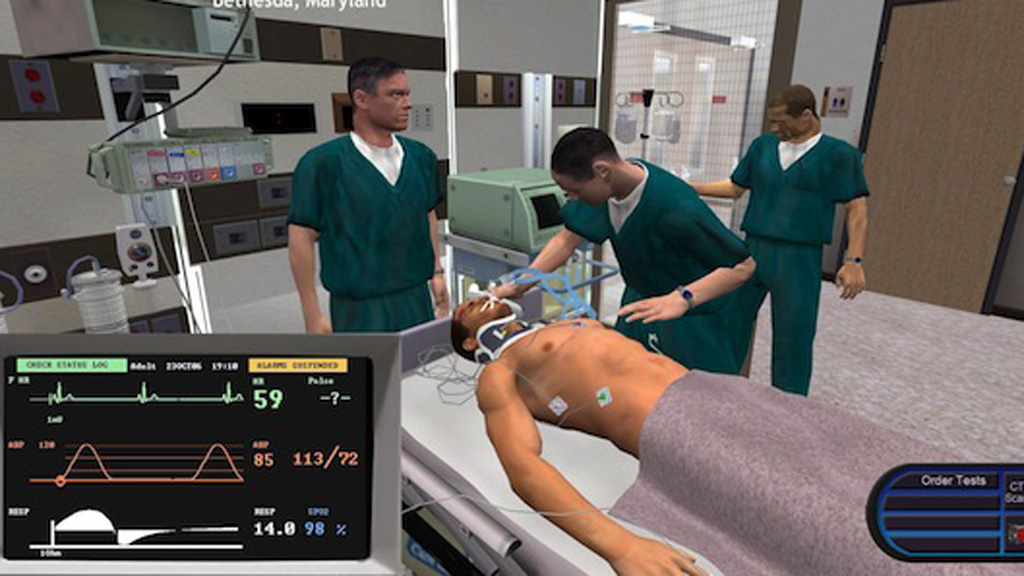
conception Assistée par Ordinateur
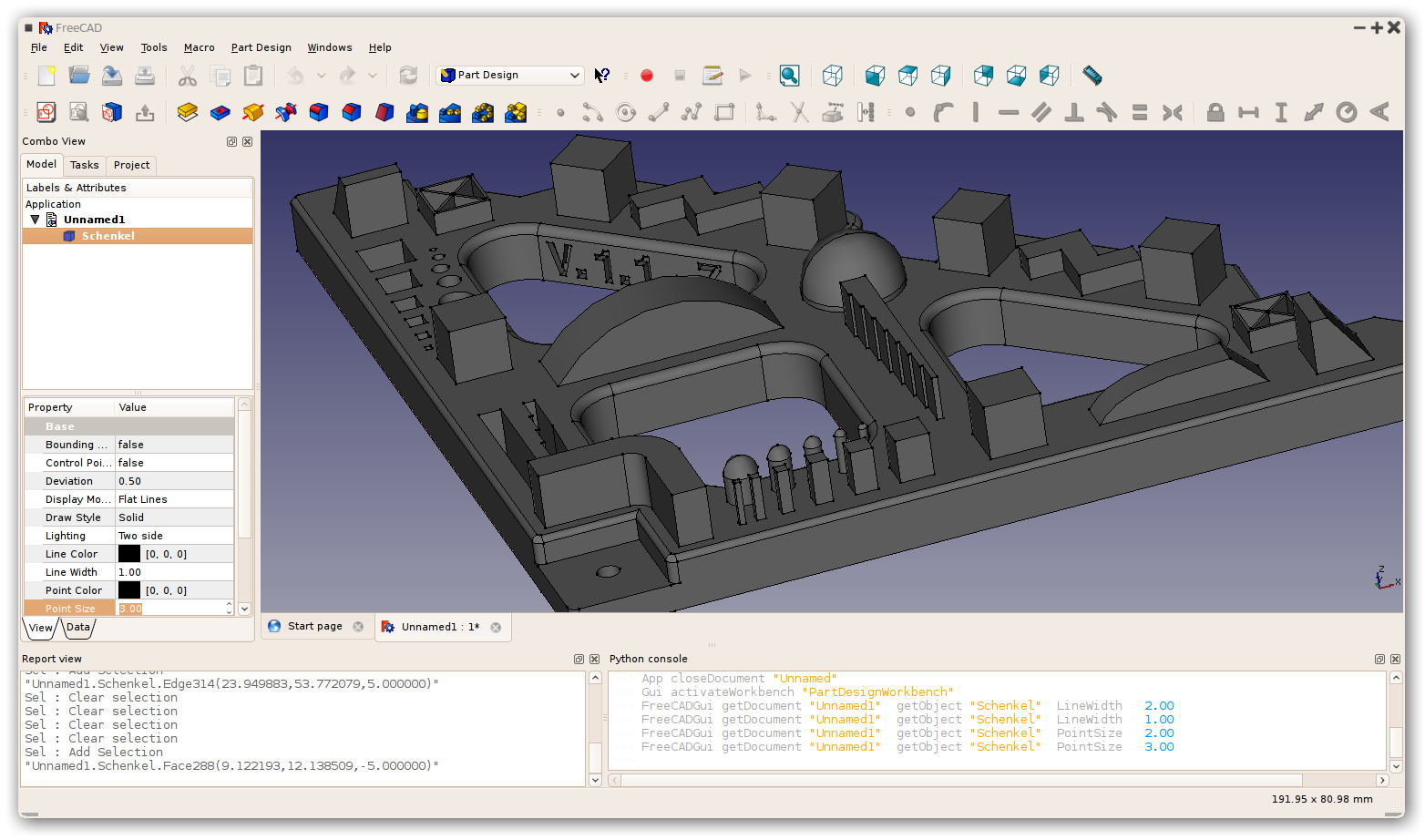
Freecad, un logiciel libre de CAO (CAD)
scanner 3D

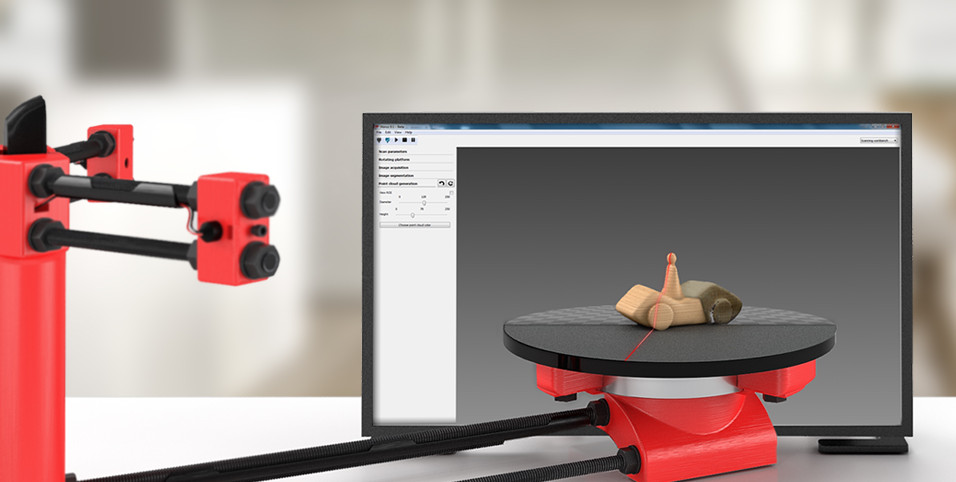
Structure de données
sous le capot, les maths
notre espace a trois dimensions

M. C. Escher. voir aussi le film Dimensions
élément géométrique élémentaire
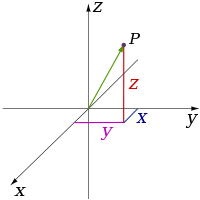
le point
Construire en 3D
on commence par ce qu'on voit
un triangle
- Par quoi est-il défini ?
- Pourquoi pas un quadrilatère ?
trois points, pas moins, et mathématiquement pas plus...
six triangles
- Combien de sommets ?
8, 10, ... 18 ? ça dépend de la topologie...
un objet décrit par des triangles
intérieur vs extérieur
l'intérieur est vide...
inversion de normales
une surface n'a de sens qu'avec une orientation
ruban de Möbius
une surface peut être non orientable
Un peu de topologie
ce qu'est une surface
ceci n'est pas une surface
une arête ne peut avoir plus de deux triangles adjacents
surface fermée, surface ouverte
voisinage en disque complet ou en demi-disque
Décrire un maillage
enfin, on en arrive à la structure de données
le plus simple : sommets et faces
OFF # cube.off # A cube 8 6 12 1.0 0.0 1.0 0.0 1.0 1.0 -1.0 0.0 1.0 0.0 -1.0 1.0 1.0 0.0 -1.0 0.0 1.0 -1.0 -1.0 0.0 -1.0 0.0 -1.0 -1.0 4 0 1 2 3 4 7 4 0 3 4 4 5 1 0 4 5 6 2 1 4 3 2 6 7 4 6 5 4 7
- formats ascii (off, obj, ply, ...)
- l'ordre des sommets donne l'orientation
- facilité de stockage
- extension possible avec textures, couleurs, voire arêtes
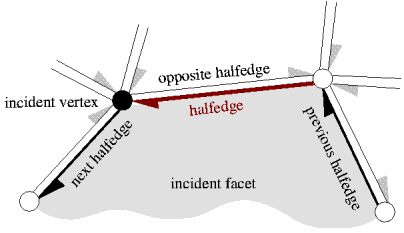
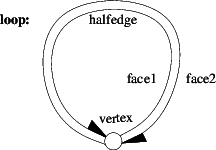
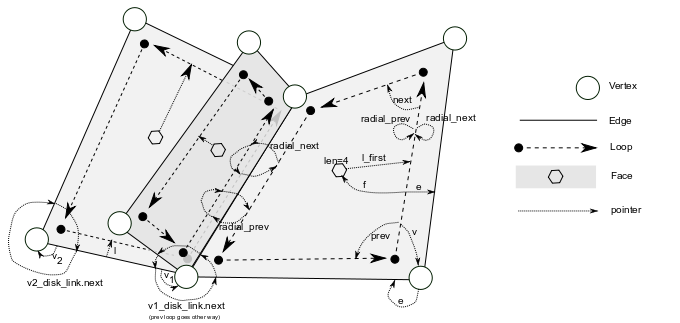
pour un parcours efficace
utilisez structure en demie-arête
Premiers algorithmes de parcours
faire des choses avec un maillage
Nombre de composantes connexes
attention, un objet peut en contenir un autre
définition
composante connexe
Un graphe non orienté S est dit connexe si quels que soient les sommets u et v de S, il existe une chaîne de u vers v. (wikipédia)
algorithme
compter le nombre de composantes connexes
- parcours en profondeur des sommets: une composante connexe
- marquage des sommets visités
- parcours de tout le graphe
Genre d'une surface
un ballon n'est pas un mug
définition
Caractéristique d'Euler
Compter le nombre de faces, arêtes et sommets d'un cube, d'un tétraèdre, d'un tore.
Calculer χ = #vertices − #edges + #faces
Calculer g = (2-χ)/2
le cas des surfaces à bord
quel changement lorsque l'on supprime une face ? deux faces adjacentes ? deux faces non adjacentes ?
χ = #vertices − #edges + #faces + #bords
comment calculer le nombre de bords ?
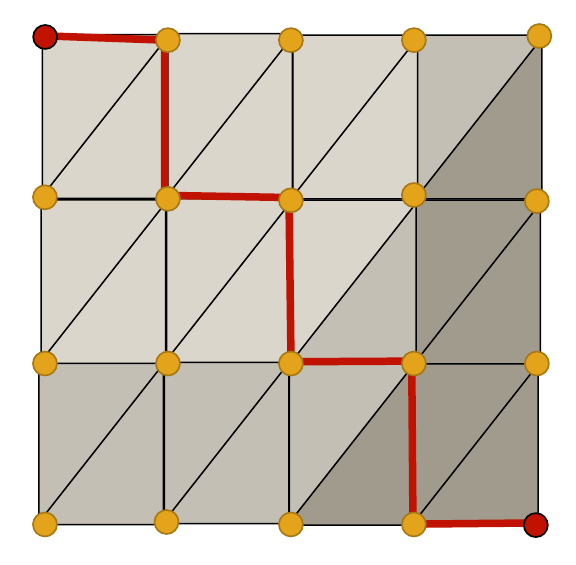
Géodésique
marcher à la surface des objets
définition
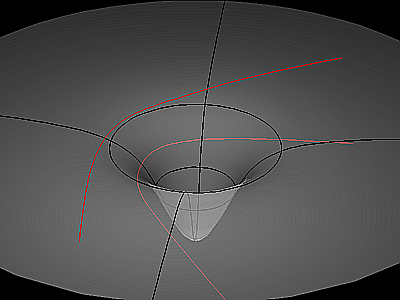
chemin géodésique
Le chemin le plus court, ou l'un des plus courts chemins s'il en existe plusieurs, entre deux points d'un espace pourvu d'une métrique est une géodésique. (wikipédia)
algorithme
approche simplifiée : le chemin d'arêtes le plus court entre deux sommets
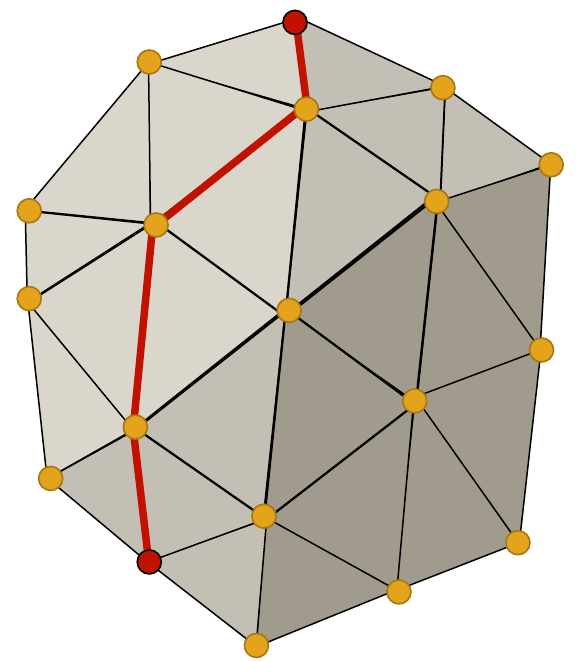
- entrée : un maillage, deux sommets
- sortie : une liste d'arêtes
- algorithme de Dijkstra
Limitations : cas de grilles dégénérées